ГРА́ФОВ ТЕО́РИЯ
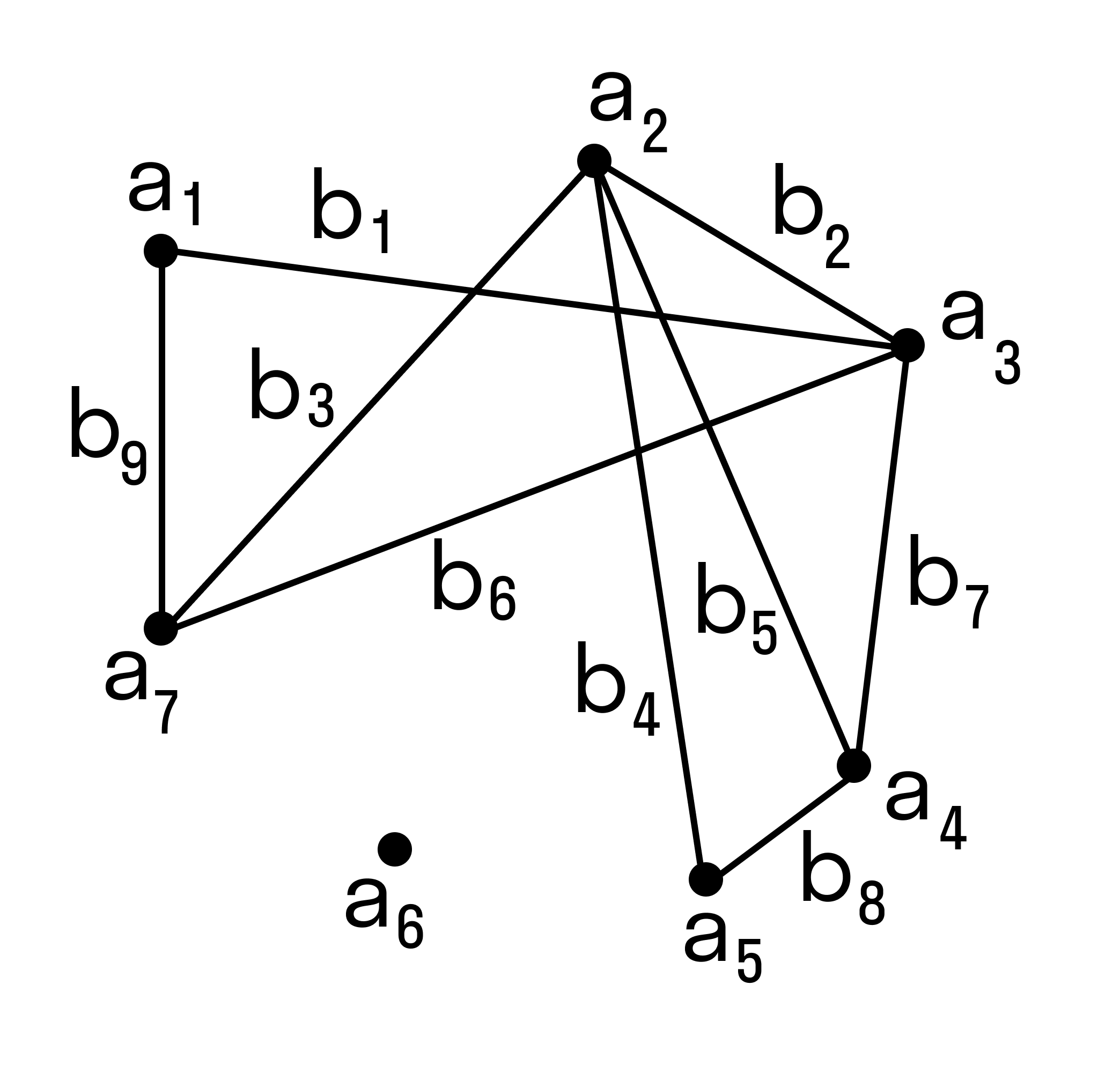
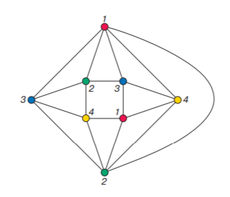
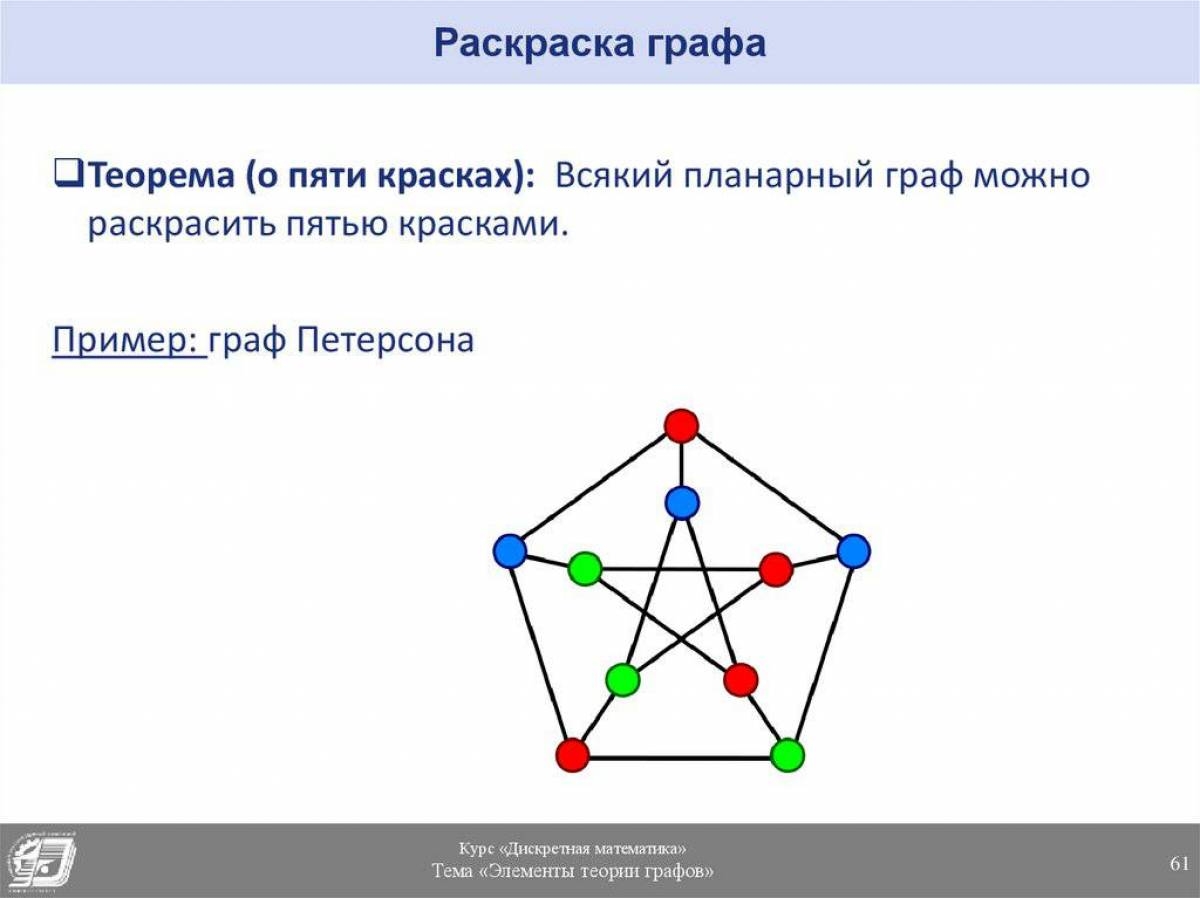
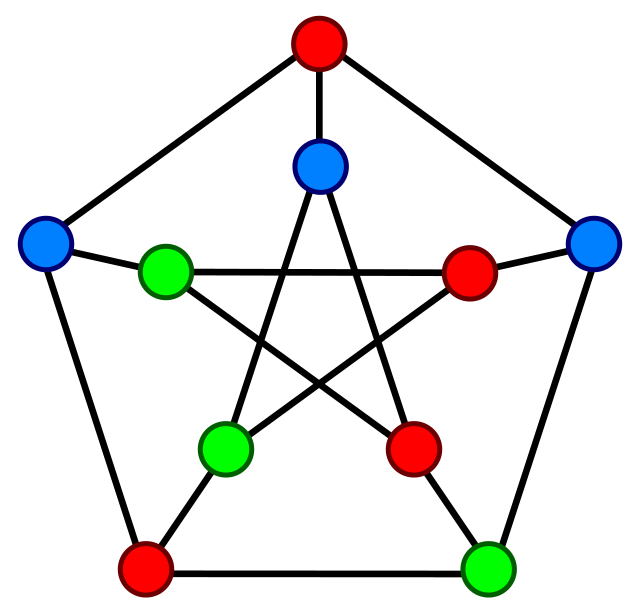
При решении практических задач с применением графов возникает необходимость в разбиении множества вершин графа на классы попарно несмежных между вершин. Довольно часто дополнительно требуется, чтобы таких классов было наименьшее число. В теории графов подобные задачи формулируются в терминах раскраски вершин графа. Параграф посвящен доказательству утверждения о том, что любой плоский граф можно раскрасить пятью красками теорема 5.




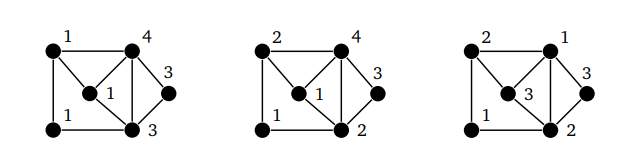


Автореферат - бесплатно , доставка 10 минут , круглосуточно, без выходных и праздников. Могильных Иван Юрьевич. Совершенные 2-раскраски графов Джонсона : диссертация Введение к работе Актуальность темы. В настоящей диссертации исследуются проблемы существования и перечисления объектов, находящихся на стыке алгебраической комбинаторики, теории кодов, исправляющих ошибки в канале связи с шумами и теории графов.



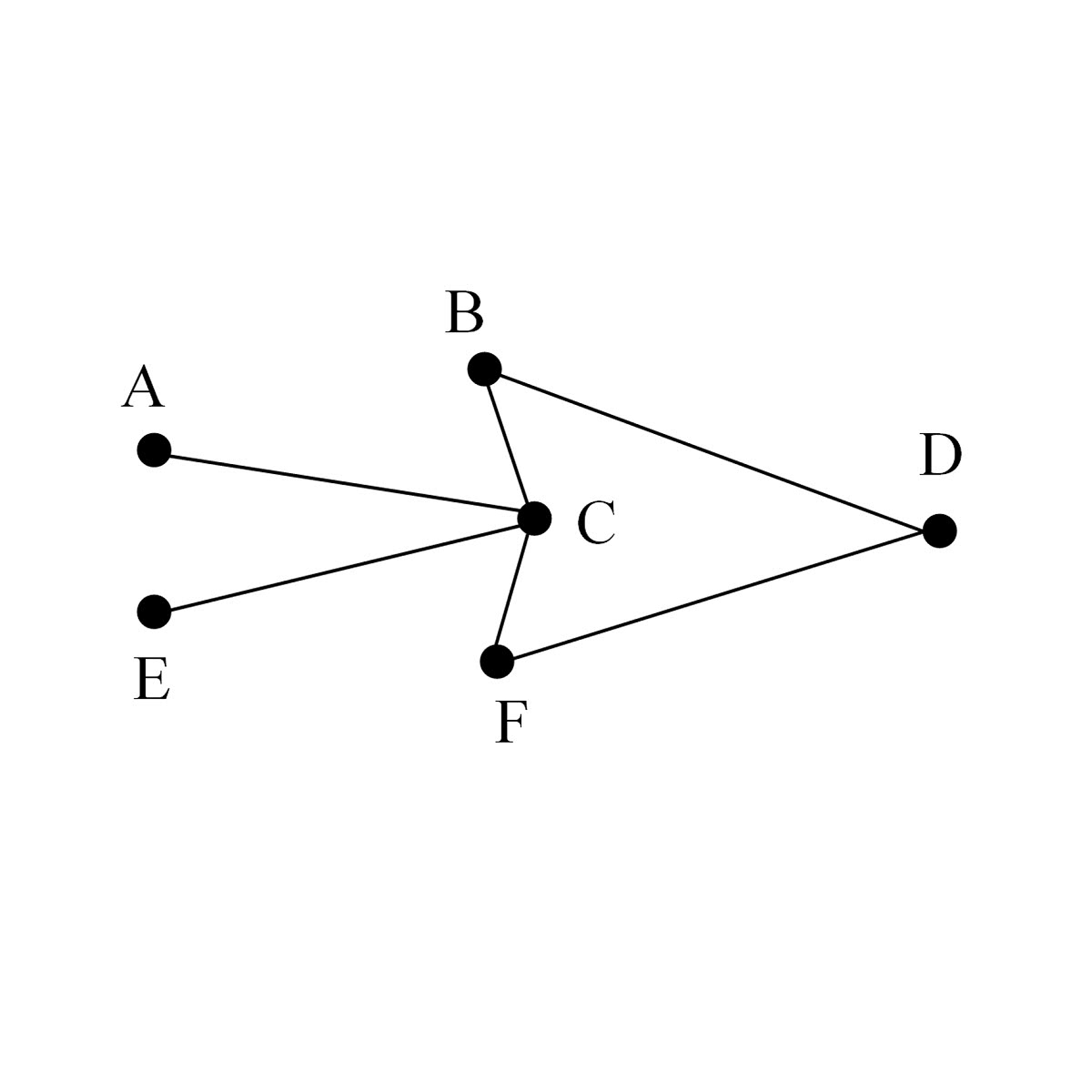




Заметим, что рассуждение теоремы Форда — Фалкерсона фактически является алгоритмом нахождения максимального потока между двумя вершинами или доказательством того, что этот поток является максимальным. Подробный пример на эту тему также приведен в разделе «Решение типовых задач». В конце этого раздела мы приведем одно полезное замечание. Если в данном графе с пропускными способностями ребер.